앞에서 Hough Transform(허프변환)을 이용하여 직선을 검출하게 되는 과정을 나타내었다.
그리고 이번 글에서는 이를 응용하여 직선이 아닌 원을 검출하게 되는 과정을 나타내어 보겠다.
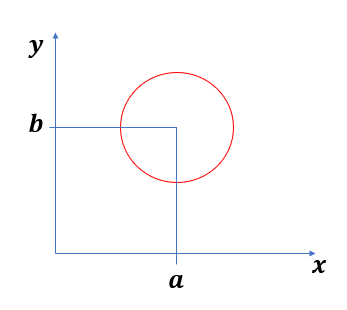
위에 흔하게 볼 수 있는 x-y평면 위에 반지름이 r인 원을 그려보았다.
이 원은 (x-a)^2 + (y-b)^2 = r^2 으로 나타내어 질 수 있다.
그럼 [그림.1]에서 그려진 붉은색 원 위의 임의의 점 P1에 대하여 생각해보자.
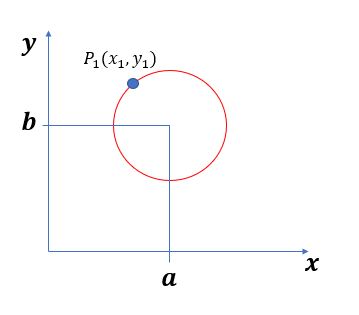
P1을 지나는 원은 굉장히 많이 존재할 것이다.
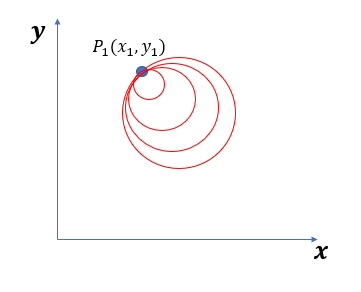
[그림.3]을 통해 볼 수 있듯이 P1을 지나는 원은 무수히 많고 각각의 원은 모두 다른 중심, 다른 반지름을 갖고있다.
즉 (x-a)^2 + (y-b)^2 = r^2 의 식에서 중심을 나타내는 a와 b, 그리고 반지름을 나타내는 r의 값이 모두
다르다는 것이다!
그럼 점 P1을 지나는 원을 타나내는 식을 써보도록 하자.
(x1, y1)의 점은 항상 포함될 것이고 a,b,r은 매개변수가 될 것이다.
앞에서 Hough Transform의 매개변수는 a와 b 로 총 2개였지만 여기서는 r까지 포함되어 3개의 매개변수,
즉 3차원으로 나타내어 지게 된다.
즉 (x-a)^2 + (y-b)^2 = r^2 의 식을 x축, y축이 아닌 a축, b축, r축에 대하여 3차원으로 나타내어 보자!
우선 식을 좀 간단하게 (a-x)^2 + (b-y)^2 = r^2 의 형태로 바꿔보자.
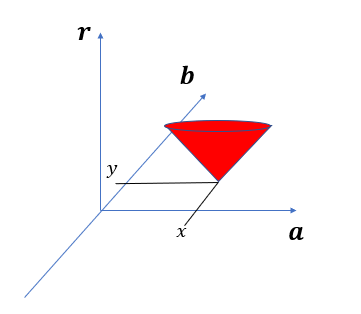
그럼 위와 같이 뒤집어진 원뿔형의 모습으로 그려지게 될 것이다.
원뿔형이 그려진다는 것에 대해 이해가 가지 않는다면
r값에 값을 하나씩 넣어보면서 생각해보자.
우선 r=0 일때 a=x, b=y 가 된다.
따라서 r축의 값은 0이되고 a의 값은 x, b의 값은 y가 되는 한 점을 나타내게 된다.
다음으로 r값에 2를 넣어보자.
(a-x)^2 + (b-y)^2 = 2^2 의 형태로 이는 중심이 (x,y)이고 반지름이 2인 원의 방정식이 된다.
즉 r축의 값이 2일땐 중심은 (x,y), 반지름은 2인 원이 그려지게 된다.
다음으로 r값에 3을 넣어보자.
위와 같은 방식으로 r축의 값이 3일때 중심은 (x,y), 반지름은 3인 원이 그려지게 된다.
이러한 과정의 반복으로 a-b-r 좌표계에는 무한히 큰 뒤집어진 원뿔형의 모습이 그려지게 된다.
그럼 이제 x-y평면상의 다른 점 P2(x2, y2)에 대하여 생각해보자.
점 P2역시 이 점을 지나는 원은 무수히 많이 존재하게 될 것이다.
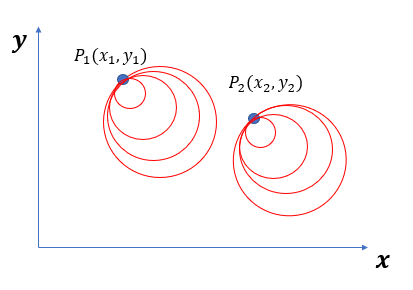
그리고 위의 과정과 똑같이 점 P2를 지나는 모든 원들을 a-b-r축을 이용하여 표시하여 보자.
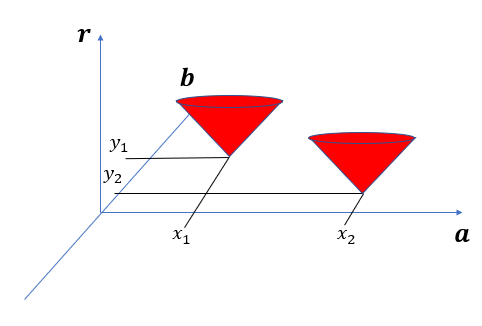
위의 [그림.6] 과 같이 나타내어질 수 있을 것이고 여기서 보이는 원뿔은 무한히 큰 원뿔이기 때문에
이때 발생되는 접점의 a,b,r값을 알 수 있고 여기에 해당하는 a,b,r값을 이용하여 x-y 평면에 나타내게 되면
P1과 P2 모두 지나게 되는 원을 그릴 수 있게 된다. ([그림.7] 참고)
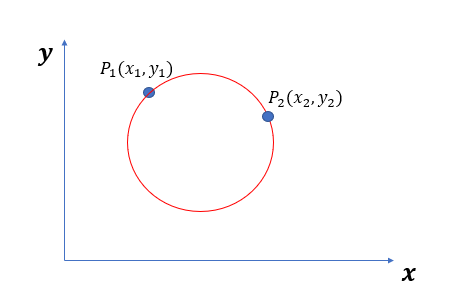
따라서 x-y평면 위의 임의의 점들이 a-b-r좌표계에서 동일한 부분에 계속적으로 겹치게 된다면
이 임의의 점들은 모두 동일한 원 위에 나타내어 진다고 볼 수 있다.
그리고 Threshold로 지정된 갯수 이상의 점들이 동일한 원 위에 있게되면 이를 원으로 판단하여 검출하게 된다.
'OpenCV' 카테고리의 다른 글
| FLIR 머신비전 카메라에 OpenCV 사용하기 (0) | 2021.05.04 |
|---|---|
| Hough Transform 을 이용한 직선 검출 (0) | 2020.12.29 |
| OpenCV 환경설정 (0) | 2020.01.08 |
| OpenCV 4.1.0환경설정(Visual Studio 2019) (0) | 2019.12.31 |
| Linux(Ubuntu)에 openCV 설치 (0) | 2019.12.26 |