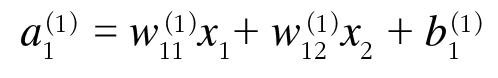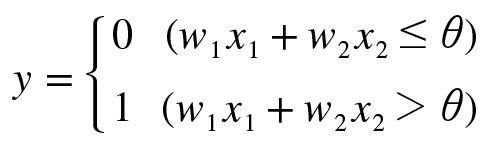선형회귀는 딥러닝의 기본이 되는 개념이지만 용어부터 굉장히 낯설어 접근하기 어렵게 생각할 수 있다.
선형회귀란 가장 훌륭한 예측선을 긋는 것으로 볼 수 있다.
예를들어 학생들의 시험 성적과 학생들이 공부한 시간과의 관계를 파악하기 위해
4명의 학생에 대해 조사하고 이를 그래프로 나타낸다고 생각해보자.
아래 그래프에서 x축 데이터는 공부한 시간, y축 데이터는 성적을 의미한다.
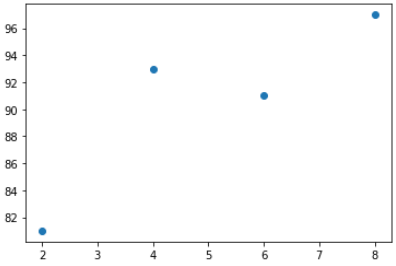
그럼 위의 그래프를 가장 잘 나타낼 수 있는 직선을 그어보자.
즉 추세선을 그어보자.
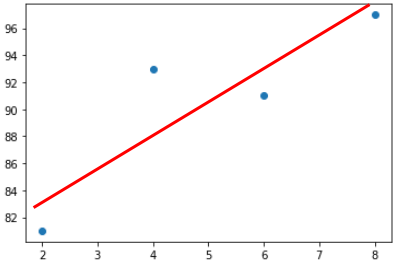
위와 같이 나타내어질 수 있을 것이다.
그럼 해당 데이터들을 가장 잘 나타낼 수 있는 추세선이 있다면 몇시간을 공부했을때 어느정도의 성적이 나올지
예측해볼 수 있다.
그럼 우리는 예측의 정확도를 향상시키기 위해 좋은 추세선을 그릴 수 있어야하고 좋은 추세선은 결국
해당되는 데이터들을 가장 잘 나타내는 선으라고 볼 수 있다.
즉 해당 데이터들을 가장 잘 나타낼 수 있는 좋은 선을 긋는 과정을 선형회귀라 볼 수 있다.
추세선을 식으로 나타내면 y=ax + b 로 표현할 수 있다.
그럼 좋은 추세선은 해당 데이터들을 가장 잘 나타내는 것이므로 오차가 가장 적은 선으로 볼 수 있고
이를 위해 최소제곱법을 사용하여 추세선 식을 나타낼 수 있다.
* 최소 제곱법
최소제곱법의 공식은 아래와 같고 이를 통해 추세선의 기울기값 a를 구할 수 있다.
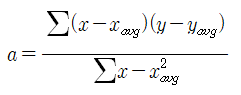
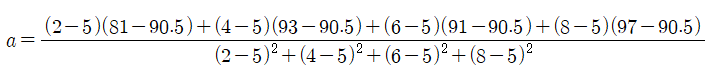
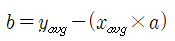
즉 위의 과정을 통해 해당 데이터를 가장 잘 나타낼 수 있는 직선을 구할 수 있고 이를 통해
임의의 x데이터에 대한 출력을 예측할 수 있다.
* 평균제곱오차
위의 방식은 한가지의 x데이터 정보에 대해서만 예측이 가능하다는 단점이 있다.
다시말해 성적에는 공부한 시간 외에도 지출한 사교육 비용, 시험 당일 컨디션, 개개인의 집중도 등이
포괄적으로 적용되어 시험성적을 나타내게 되는데 최소제곱법을 통해서는 하나의 조건에 대해서만
예측이 가능하다는 단점을 지니고 있다.
그리고 이를 위한 방법으로 평균제곱오차를 다뤄보겠다.
이 방법은 일단 추세선을 그리고 조금씩 변화시켜가며 정확한 추세선을 찾아가는 과정이라 볼 수 있다.
이러한 과정을 통해 입력데이터가 여러 종류일때에도 적용하여 출력값을 추정할 수 있다.
하지만 이 과정을 진행하기 위해선 나중에 조금 변화시킨 추세선이 이전의 추세선보다 우수한 선임을
판단할 수 있어야한다.
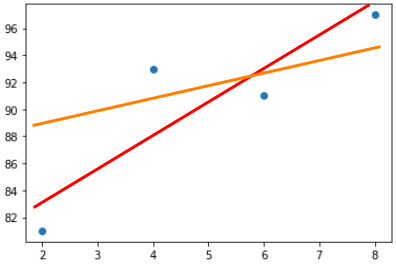
만약 위의 그래프에서 붉은색으로 나타낸 직선이 가장 우수한 추세선이라고 가정해보자.
평균제곱오차 방식을 사용하기 위해 임의의 직선을 하나 그어보자(이는 주황색으로 표시하였다).
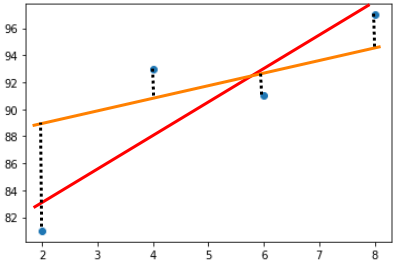
그리고 어느정도의 오차가 발생하였는지 파악할 수 있어야 어떠한 직선이 더 우수한 직선인지 판단할 수 있으므로
위와 같이 해당 데이터에서의 실제 출력값과 추세선으로 추정된 값과의 차이를 확인한다
점선으로 표시된 직선들의 합이 클수록 잘못 그어진 추세선이고 작을수록 잘 그려진 추세선이라고 판단할 수 있다.
오차는 (예측값)-(실제값)으로 표현될 수 있지만 위의 경우를 보면 어떠한 경우는
예측값이 실제값보다 커서 오차가 양수를 갖지만 예측값이 실제값보다 작은 경우에는 오차가 음수를
갖게되어 무작정 오차를 합하게 되면 무의미한 오차값이 될 수 있고 따라서 부호를 없애주는 작업을
진행하여준다.
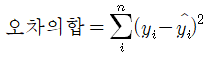
그리고 x데이터의 개수로 나누어 오차 합의 평균을 구하면 이를 평균 제곱 오차(Mean Squared Error, MSE)라
하고 다음과 같이 표시한다.
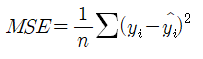
* 경사 하강법
그럼 평균제곱오차를 통해 두 직선에 대해 어느 직선이 더 우수한지 비교할 수 있는 과정을 진행하였다.
그리고 처음에는 임의의 값을 통해 진행할 수 있었다.
하지만 정말 터무니없는 직선들을 가져와 비교해보며 최적의 추세선을 찾기에는 굉장히 노가다스러움이
느껴지고 연산량도 굉장히 많아질 수 있을 것이다.
이를 해결하기 위해 초기 임의의 직선과 그 다음 직선을 선택하는 과정을 경사 하강법을 통해 살펴보자.
'Deep Learning' 카테고리의 다른 글
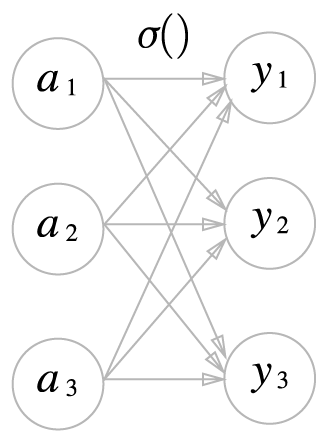
| 신경망 활성화 함수(계단함수, 시그모이드 함수, 소프트맥스 함수) (0) | 2020.02.04 |
|---|---|
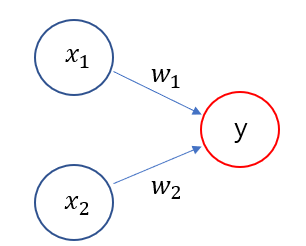
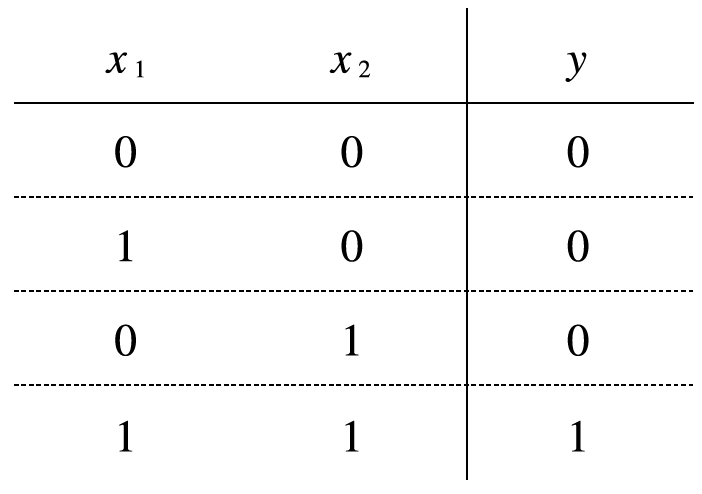
| 퍼셉트론(Perceptron) (0) | 2020.02.04 |