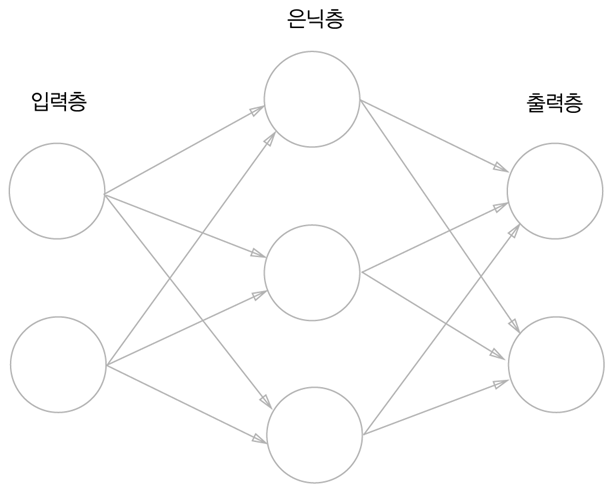
신경망을 그림으로 나타내면 위의 그림과 같고 입력층, 은닉층, 출력층으로 이루어진 것을 볼 수 있다.
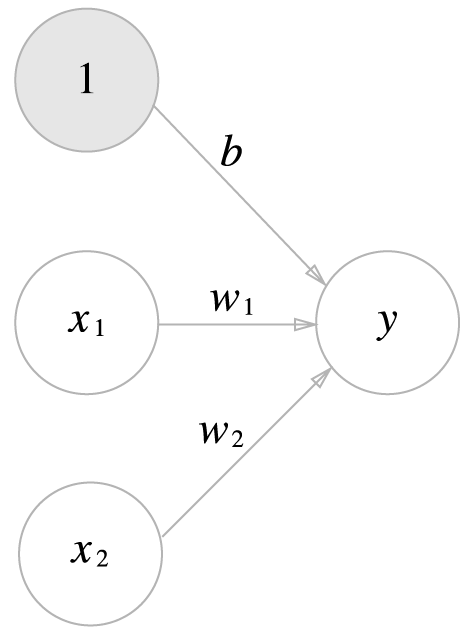
x1과 x2 의 신호를 입력으로 받아 y를 출력하는 퍼셉트론은 위의 [그림.2] 와 같이 표현될 수 있고
이를 식으로 표현하면 아래와 같다.
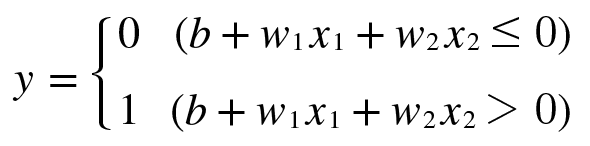
여기서 b는 편향을 나타내는 매개변수로 뉴런이 얼마나 쉽게 활성화되느냐를 제어하게 되고
w1과 w2는 각 신호의 가중치를 나타내는 매개변수로 각 신호의 영향력을 제어하게 된다.
그리고 이 식을 변형시켜서 아래와 같이 표현할 수 있다.
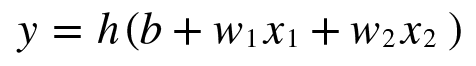
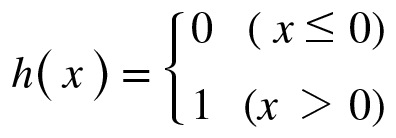
즉 (b+w1x1+w2x2) 가 0보다 작거나 같으면 0, 0보다 크면 1 이므로
[식.1] 은 [식.2]와 [식.3] 으로 표현될 수 있다.
이 때, 함수 h(x)를 활성화함수 라 하고 입력신호의 총 합을 출력신호로 변환시키는 작업을 하게 되는 함수이다.
따라서 위 [식.2], [식.3] 은
[식.2] -> 가중치가 곱해진 입력신호의 총 합을 계산함
[식.3] -> 그 합을 활성화함수에 입력해 결과를 나타냄
위의 2가지 과정으로 진행이 되고 따라서 아래와 같이 표현이 가능하다.
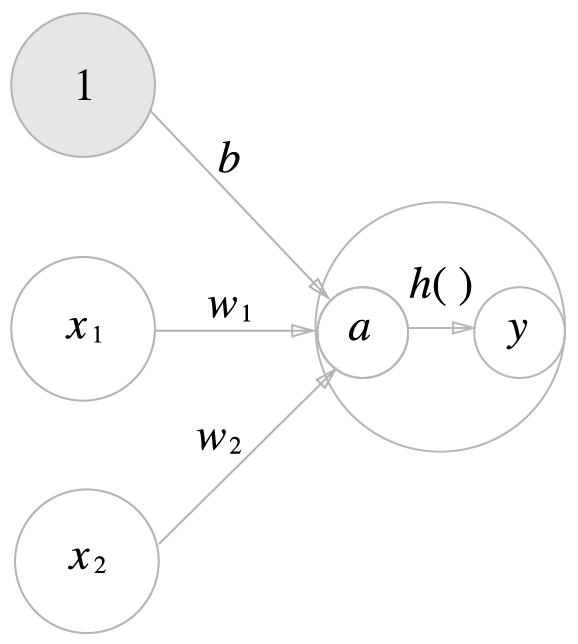
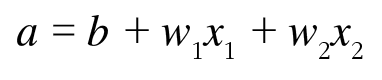
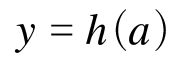
즉 a는 입력신호와 가중치를 합한 값
h(a) 는 a의 값에따라 결과적으로 1인지 0인지를 판별하는 과정을 진행하는 함수
로 정리할 수 있다.
위의 [식.2], [식.3] 을 확인하여보면 x값에 따른 결과(h(x))가 0 아니면 1을 갖게 되고 이를 그래프로 표시하면
계단함수형태를 나타내게 된다.
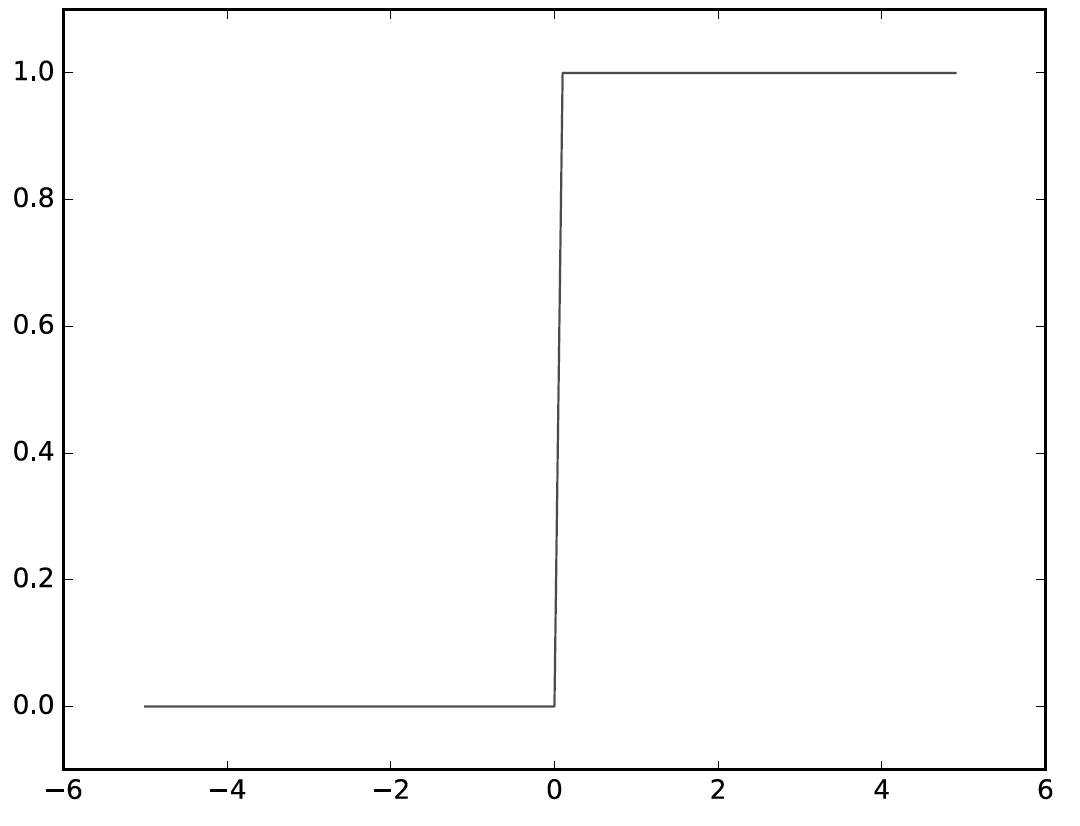
여기까지의 내용은 퍼셉트론에서 다룬 내용과 비슷하다.
퍼셉트론과 신경망의 가장 큰 차이는 활성화 함수 h(x)이고 h(x)의 형태가 퍼셉트론의 경우 위와같은 계단함수 형태,
신경망의 경우 부드러운 곡선형의 시그모이드 함수의 형태를 갖게 된다.
시그모이드 함수란
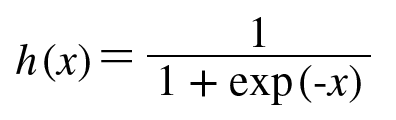
활성화 함수 h(x)의 값이 다음과 같이 표시되고 그래프로 나타내게 되면
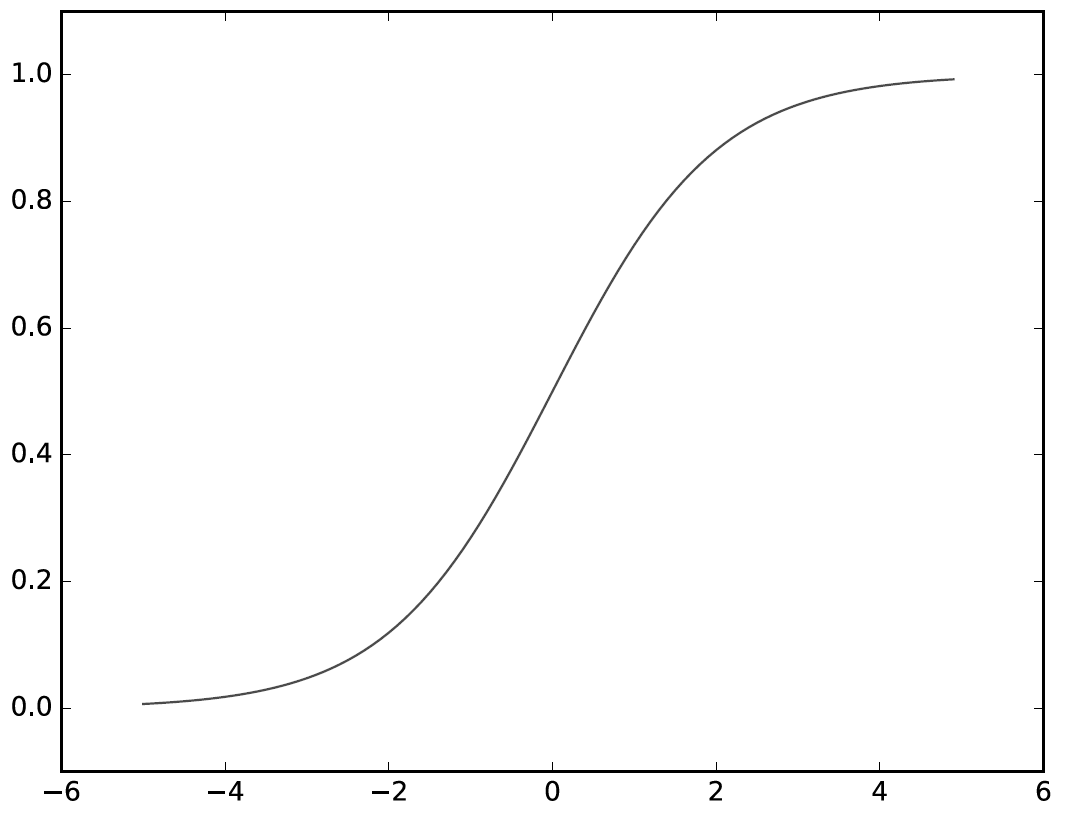
위의 [그림.5]와 같이 부드러운 곡선 형태로 그려지게 된다.
한가지 짚고 넘어갈 것은 계단함수와 시그모이드 함수 모두 비선형 함수라는 것이다.
선형함수는 층을 아무리 깊게해도 은닉층이 없는 네트워크로 표현되기 때문에 비선형함수이어야 한다.
* 참고 *
시그모이드 함수는 신경망 분야에서 오래전부터 사용되었으나 최근에는 ReLU함수를 주로 사용하고 있다.
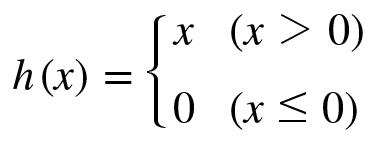
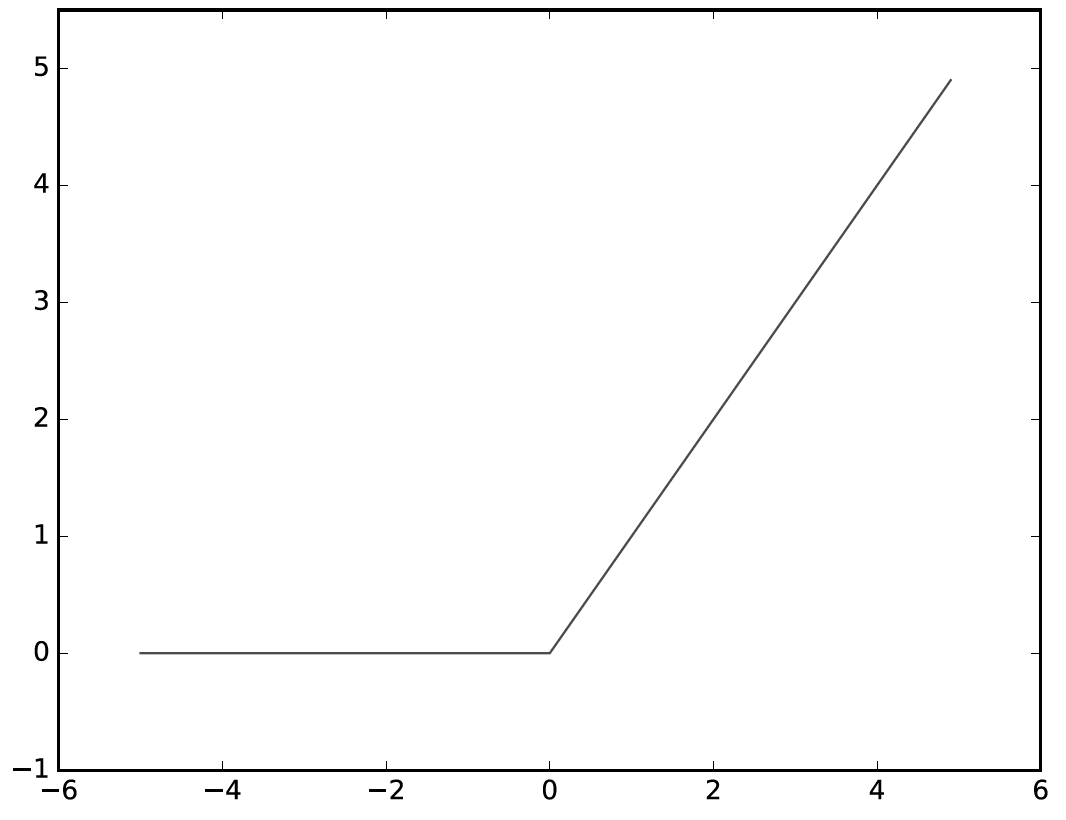
그럼 이제 신경망을 구현하여 보자.
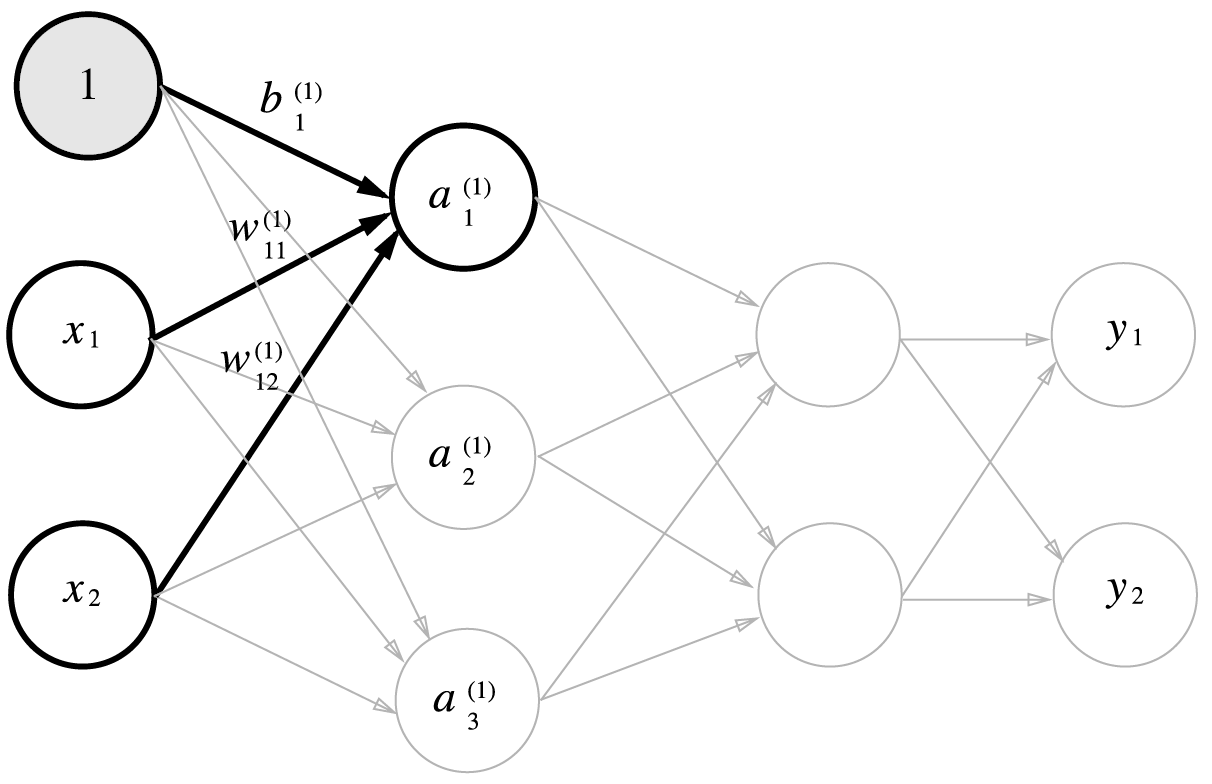
위의 그림을 보면 편향과 입력값(x1, x2)을 이용하여 1층의 a1 값을 구하게 된다.
이와같은 방식으로 1층의 a2, a3를 구할 수 있을 것이고 여기서 구한 a값을 이용하여
그 다음 2층의 a1, a2값을 구할 수 있게 된다.
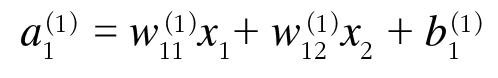
즉 위와 같이 a1이 표현될 수 있고 이 과정을 계속 진행하여 1층의 a원소들은 행렬 A로 아래와 같이 표현된다.
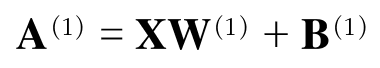
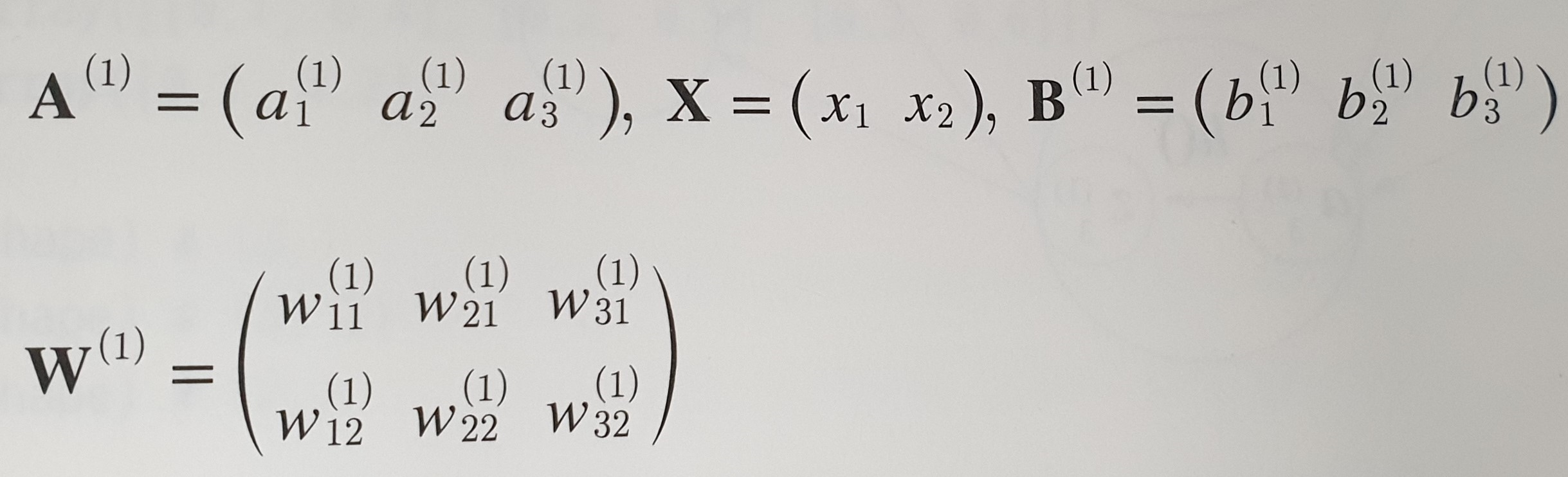
2층, 3층의 계산 과정은 아래의 그림을 참고하도록 하자.
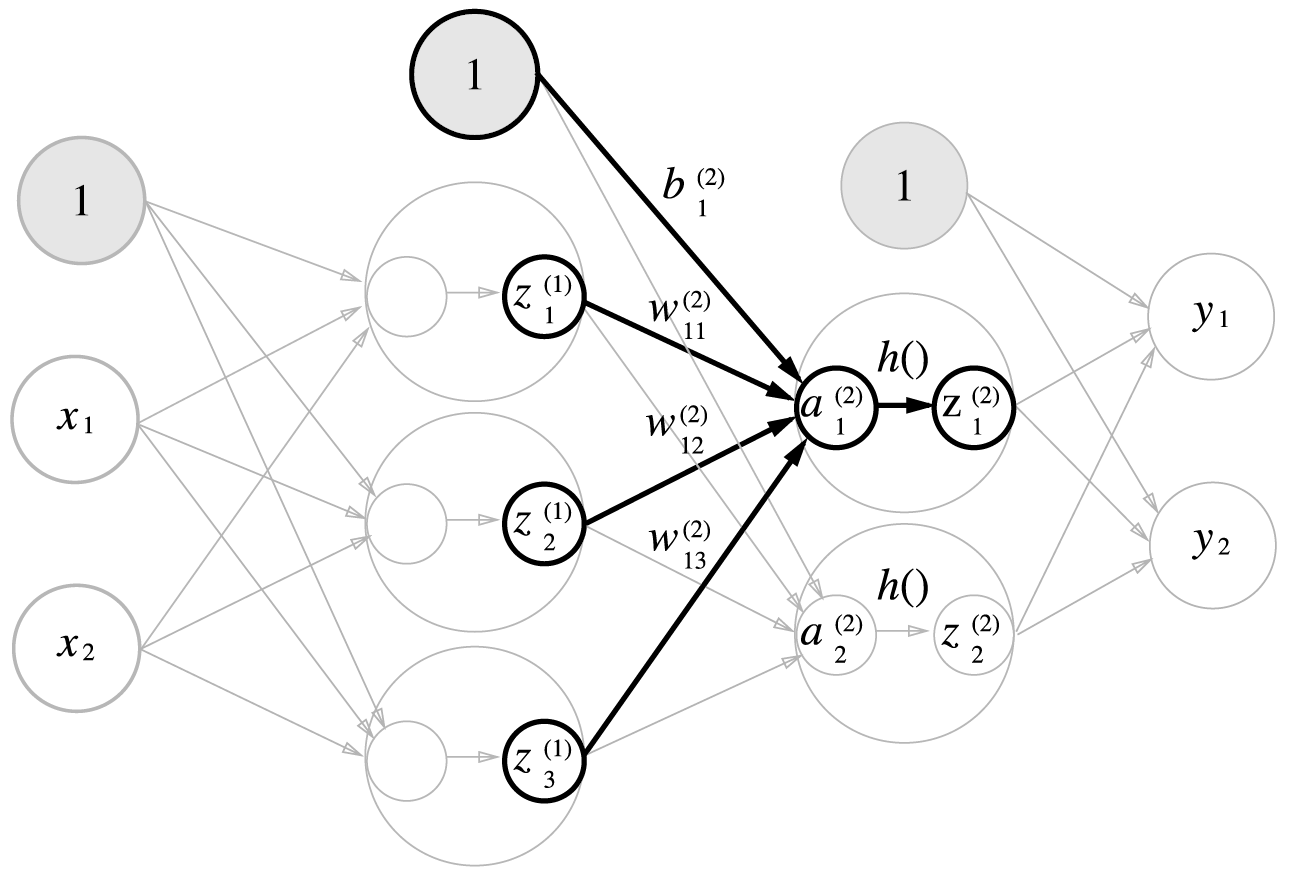
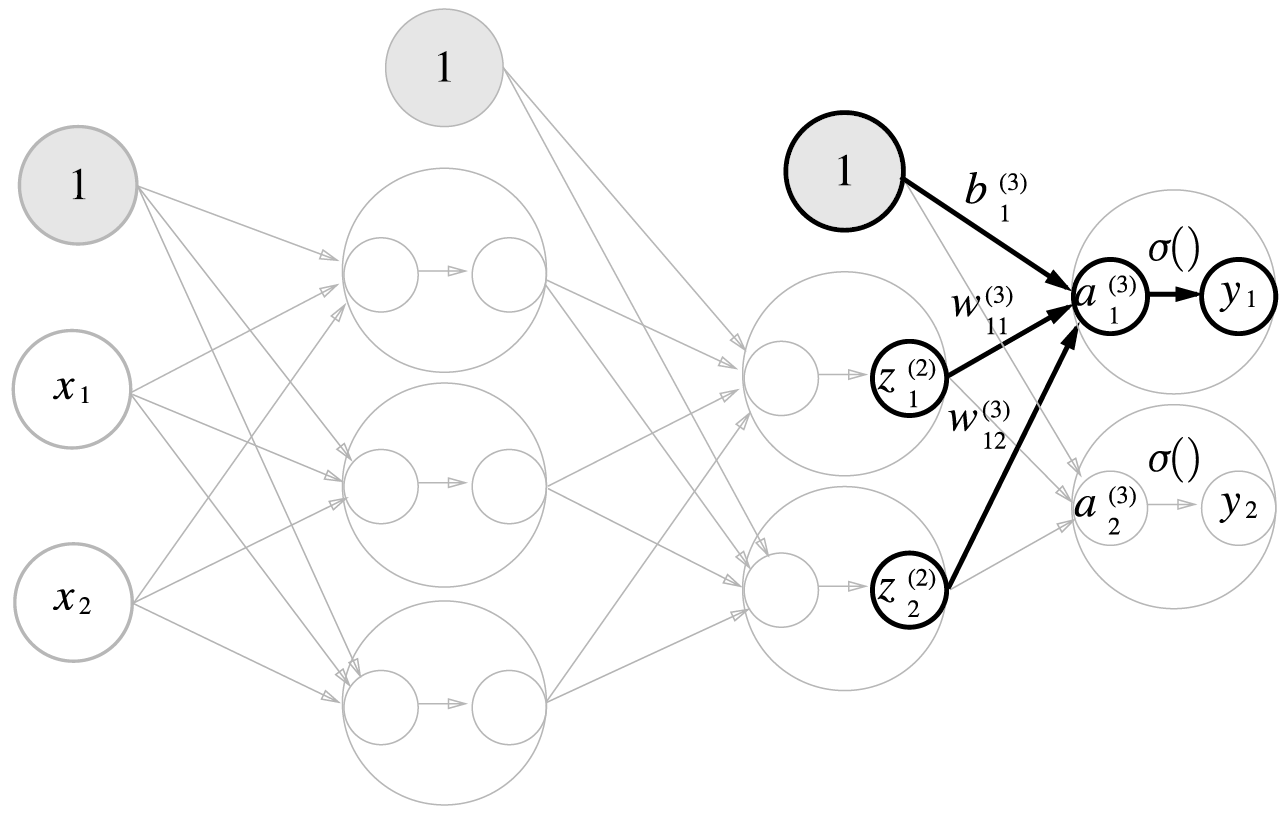
### 입력층에서 1층으로까지의 과정
X = np.array([1.0, 0.5])
S1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
B1 = np.array([0.1, 0.2, 0.3])
print(W1.shape)
print(X.shape)
print(B1.shape)
A1 = np.dot(X, W1) + B1
Z1 = sigmoid(A1)
print(A1)
print(Z1)
### 1층에서 2층으로까지의 과정
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
B2 = np.array([0.1, 0.2])
print(Z1.shape)
print(W2.shape)
print(B2.shape)
A2 = np.dot(Z1, W2) + B2
Z2 = sigmoid(A2)
### 2층에서 출력층으로까지의 과정
def identity_function(x): ## 여기서 identity 함수는 입력값을 그대로 출력하게 되는 함수
return x
W3 = np.array([[0.1, 0.3], [0.2, 0.4]])
B3 = np.array([0.1, 0.2])
A3 = np.dot(Z2, W3) + B3
Y = identity_function(A3)
그 다음 등장하는 개념은 분류에서 사용되는 소프트맥스 함수(Softmax function) 이다.
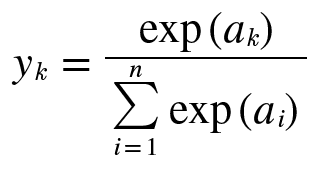
위의 식에서 n은 출력층의 뉴런 수, y_k 는 그 중 k번째 출력임을 뜻하고 있다.
이를 그림으로 나타내면 아래와 같다.
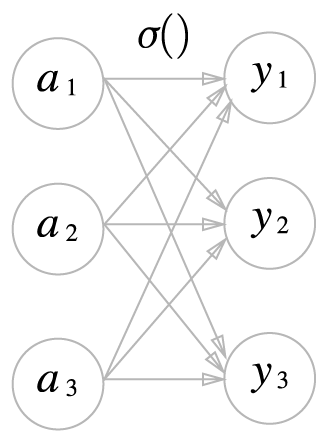
이를 보면 소프트맥스 함수의 출력은 모든 입력 신호로부터 화살표를 받게 된다.
즉 출력층의 각 뉴런이 모든 입력신호에서 영향을 받는다는 것을 확인할 수 있다.
하지만 위의 소프트맥스 함수[식.8]은 지수함수로 이루어져 k의 값이 굉장히 커지게 되면 오버플로우가 발생하게 된다.
(컴퓨터는 수를 4바이트나 8바이트와 같이 크기가 유한한 데이터로 다루기에 표현할 수 있는 수의 범위가 한정적이다)
이를 확인하기 위해 프롬프트창에서 다음과 같이 실행시켜보자.
>>> a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a))
이를 실행시키면
array([ nan, nan, nan])
과 같이 출력될 것이다.
그럼
위의 내용에 이어서
>>> c=np.max(a)
>>> a-c
를 입력하면
array([0, -10, -20])
이 출력되는 것을 확인할 수 있고 계속 이어서
>>> np.exp(a-c) / np.sum(np.exp(a-c))
를 입력하여 확인하여보면
array([ 9.99954600e-01, 4.53978686e-05, 2.06106005e-09 ])
의 값이 출력되는 것을 확인할 수 있다.
즉 간단하게 표현하여
def softmax(a):
c=np.max(a)
exp_a = np.exp(a-c)
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
위와 같이 구현할 수 있다.
소프트맥스 함수의 큰 특징은 이를 이용하여 소프트맥스 함수의 결과값을 확률로 해석할 수 있다는 것이다.
소프트맥스 함수의 결과값은 0에서 1.0 사이의 실수이다.
또한 출력의 총합이 1이 되고 출력값이 모든 입력값의 영향을 받기때문에 확률로 해석이 가능하다.
또한 소프트맥스 함수를 적용해도 y=exp(x)의 함수는 단조증가함수이기에
각 원소의 대소관계는 변하지 않는다.
'Deep Learning' 카테고리의 다른 글
| 선형회귀 (0) | 2021.01.11 |
|---|---|
| 퍼셉트론(Perceptron) (0) | 2020.02.04 |